70年代初西门子工程师F.Blaaschke在读博士期间，其导师给他出了一个课题，就是如何通过运算来实现交流电机的直流化控制。（因为直流电机的励磁和电枢部分单独实现调节，在励磁恒定的情况下，只需控制直流电机的电枢电流即可实现对电机转矩的控制，而交流电动机则不同。根据公式3可知。）交流电动机的磁通和电流是耦合在一起的，改变磁通的同时会同时引起电流的变化。F.Blaaschke想出一个非常天才的想法，即通过坐标变换先将电动机的三相系统等效为两相系统，再经过按转子磁场定向的同步旋转变换实现定子电流励磁分量与转矩分量之间的解耦，从而达到对交流电机的磁通和电流分别控制的目的，这样就可以将一台三相异步电机等效为直流电机来控制，因而获得与直流调速系统同样的静、动态性能，一举打破了直流调速系统一统天下的局面。

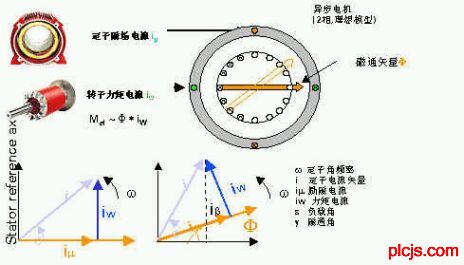
七十年代初期，西门子公司的FBlaschke和WFlotor提出了“感应电机磁场定向的控制原理”，通过矢量旋转变换和转子磁场定向，将定子电流按转子磁链空间方向分解成为励磁分量和转矩分量，得到类似于直流电机的数学模型。1980年，日本ANabas教授和山村昌教授提出转差矢量控制系统。直到现在，科学家仍在进行着不懈的研究。

仿真分析是解决矢量控制系统复杂性问题的有力手段，为此，本文根据矢量控制系统的构成框图，建立了面向结构图的电流滞环型矢量控制交流调速系统的一体化仿真模型，并用MATLAB的Simulink语言，直接进行仿真，得到了良好的效果。同时，该仿真模型可以直接作为平台对调速系统的控制器、电流变换和磁链观测器、电流控制变频器及异步电动机等模块进行检验和比较，具有很好的通用性。

1 系统的组成

本文所用的仿真系统为转速、磁链闭环电流滞环型PWM变频调速系统，为了提高系统的快速性和限流的必要性，电流调节器采用传统的PI调节器。同时为了保持系统的通用性，转速和转矩调节器亦采用PI调节器，系统的原理框图如图1所示。

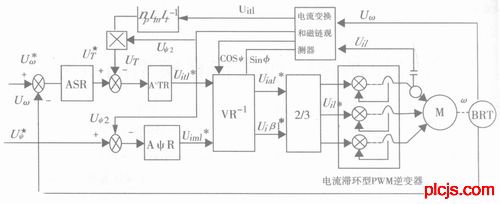
图1 转速、磁链闭环电流滞环型PWM变频调速系统

ASR-速度调节器；ATR-转矩调节器；AΨR-磁链调节器；BRT-速度传感器

转速、磁链闭环电流滞环型调速系统其简化构成框图如图2所示。

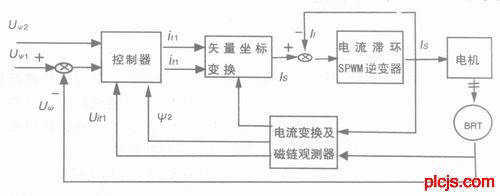
图2 矢量变频调速系统的一体化仿真模型

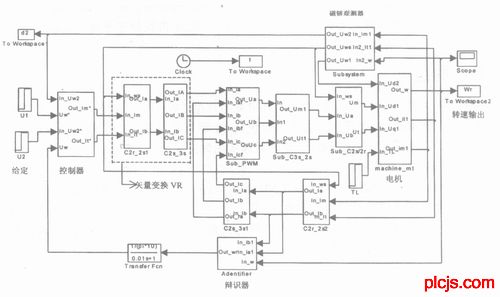
图2附图 矢量控制系统的通用仿真模型

图中各模块在MATLAB的SIMULNK下均可以由相应的单元模块构成，控制器和矢量坐标变换部分有现成的数学模型或构成图，易于实现，为此，下面仅给出了难于建模的电流控制变频器、电流变换磁链观测器及异步电动机的仿真结构图。在仿真过程中，将各模型块的输入输出端口顺序连接即可进行仿真。

2 仿真模型的建立

2.1 电机仿真模型

图2附图矢量控制系统的通用仿真模型

电机仿真模型采用按转子磁场定向二相同步旋转坐标系下的数学模型：

电压方程：

(1)

磁链方程：

Ψ_m1=L₁i_m1+L_mi_m2

Ψ_t1=L₁i_t1+L_mi_t2 (2)

Ψ_m2=L_mi_m1+L₂i_m2=Ψ₂

Ψ_t2=L_mi_t1+L₂i_t2=0

转矩方程：

T_e=N_pL₂^-1LmΨ₂i_t1 (3)

运动方程：

Te-T₁=N_p^-1Jdωr/dt (4)

式(1)～(4)中：

R₁、R₂ 定转子电阻L₁=L_σ1+L_mL₂=L_σ2+L_mL_σ1

L_σ2 定转子漏感

L_m 定转子间互感 L₁L₂ 定转子自感 ω₁ 电机同步角频率

ω_s 电机转差角频率 ω_t 电机转子电气角速度 u_m1u_t1 MT轴定子电压

u_m2u_t2 MT系转子电压 i_m1i_t1 MT系定子电流 i_m2i_t2 MT系转子电流

Ψ₂ 转子总磁通 T_e 电磁转矩T₁ 负载转矩 N_p 电机极对数

J 机组转动惯量

显然，直接对该数学模型进行仿真是不方便的，为此需要选择恰当的状态变量进行变换，以防止模型中出现微分环节，导致电机和系统的不稳定。变换过程参考文献［2］，从而可得电机的仿真模型如下：

其中：

R=R₁+L₂^-2L_m² L_σ=L₁-L₂^-1L_m^2

A=L₂^-2L_mR₂ B=L₂^-1L_m

C=L₂^-1L_mR₂ D=L₂^-1L_mN_p E=L_m^-1R₂^-1L₂

G₁(S)=1/(R+L₀S) G₂(S)=1/(L₂^-1R₂+S)

二相电压U_m1和U_t1由三相定子电压经C_3s/2s和C_2s/2r变换得到。

2.2 电流控制型SPWM逆变器仿真模型

假定电流滞环控制逆变器由稳定的直流电源供电，考虑逆变器所带来的滞后，则由文献［1］中电流滞环控制SPWM逆变器的控制原理框图可得其仿真结构图如图4所示：

图中的滞环比较器，当i_a-i_af＞1，输出为1，若i_a-i_af＜-1，输出为-1，否则输出保持不变。K取值300，T_d为逆变器滞后时间常数(取值0002S)，功率放大环节为带有限幅的放大器，正负限幅值为300 V。输出直经C_3s/2s和C_2s/2r变换后对电机模型直接供电。

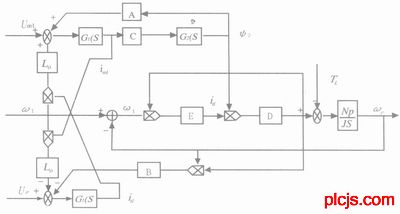
图3 异步电动机在二相同步旋转坐标系(MT系)下的仿真模型

2.3 电流变换及磁链观测器仿真模型

该仿真模型采用文献［2］中磁场定向二相旋转坐标系下的运算框图，由该框图可得仿真结构图

如图5所示。

图4 电流滞环SPWM逆变器仿真模型图   5 电流变换及磁链观测器仿真模型

图中，f(u)，g(u)为Fcn函数，Mux为矢量合成模块， f(u)=10^-5+sign(u)^*10^-6，以防止在g(u)中被除函数为0造成仿真停止，g(u)=L_mu₁/(T₂u₂)，G₃(S)=。

2.4控制器中调节器的取值

ASR、ACR及ATR均采用PI调节器，参数如下：

速度调节器(ASR)：(k_p1+k₁₁/S) K_p1=5,K₁₁=15，正负限幅为10V。

磁链调节器(AΨR)：(K_p2+K₁₂/S) K_p2=5，K₁₂=15，正负限幅为10V。

转矩调节器(ATR)：(K_p3+k₁₃/S) K_p3=5，K₁₃=10。

3仿真研究及结果

系统仿真采用MATLAB面向结构图的Simulink仿真软件。为验证系统的有效性，现以实际电机为例，对其进行仿真。电机参数如下：

P=1.7 kw，L_nom=3.86 A， T_cnom=11.35 N·m，n_nom=1430r/min，cosφ=0.82，η=87.5%， R₁=4.1 Ω，R₂=25 Ω，L_σ1=0.035 H，L_m=0.510H，N_p=2，J=0.02 kg·m²。

打开simulink仿真软件，建立各模块的模型并将其顺序连接，即可构成矢量变频调速系统的一体化仿真模型。

首先，考虑系统的启动特性，系统在值50π(rad/s)的作用下空载起动，2秒后，转速给定值突加到100π(rad/s)。仿真计算出的转速ω及磁通Ψ₂的变化曲线如图(6)所示。再考虑系统的抗干扰性能，电机在空载下启动，1.5秒后，电机突加额定负载11.35 N·m，再过2S后，电机负载突然减到4 Nm。仿真计算出的转速ω及磁通Ψ