点击: 作者:未知
要实现一个完整的基于摄像头的智能小车,第一步要做的就是将摄像头输出的模拟信号通过单片机A/D转换采集到单片机中,然后对采集到的原始的图像数据进行处理,以获取赛道中央的黑线在图像坐标系中的位置。
接着,就要利用处理得到的图象信息对智能小车进行控制。就目前而言,各参赛队用的最多的横向控制(转向控制)就是PID控制。采用PID控制方式,无需对摄像头作严格的标定,因为只须将黑线在图像坐标系中的位置偏差乘相应的PID系数,就可以作为转向的控制律,至于PID系数取多少,则可以通过简单的实验调试而获得合适的取值。正因为这样,PID控制方式简单易行。
而PID控制方式却有其局限性,其最大的局限性就是无法很好控制智能小车的行驶线路(简称“走线”)。PID参数的变化会引起小车走线的变化,即使 PID参数相同的情况下,小车速度的或高或低同样会引起小车走线的变化。这样,因为小车走线的不确定性,为了比赛时小车不冲出赛道,只有尽量控制小车完全沿线行驶,这样才能使小车无论在左侧还是右侧都有较充足的赛道裕量。但另一方面,完全沿着赛道中央黑线的走线也许并不是最优的走线,比如,在一些特殊路段抄近道,可能
基本思路
预测控制的基本思想是:在每一控制周期内,通过摄像头获取车前方一定区域内黑线的位置信息——与PID控制方式不同的是,预测控制多了摄像头标定这一步,即将黑线在图像坐标系下的位置转换成世界坐标系下的位置——然后规划出一条较优化的走线,成为期望走线。然后根据小车的运动学模型和转向模型可以确定(一种最优化问题求解的过程),在往下若干个控制周期内,转角控制量依次取多少时,小车走线才能最“接近”规划出的期望走线。仅仅选取求解出的当前控制周期的转角控制量作为实际的转角控制量。在下一周期,将重新进行一次上述的规划、最优化求解过程,如此反复循环执行下去。具体介绍如下文所示。
摄像头标定
因为要进行走线规划,就得获取黑线的实际位置信息。通过摄像头所获得的只是黑线在图像坐标系下的位置。因此,首先得求出图像坐标系到世界坐标系的变换关系,这个变换关系是一个仿射变换关系,可以事先写出这个变换关系的形式,然后再取一些标定样点,通过计算标定出这个变换关系形式中的各个参数。摄像头标定因为不作为本文重点,受篇幅所限,具体细节不在此赘述。
走线规划
在赛车比赛中,走线选取的好坏可以作为评价车手水平高低的一个标准。在智能小车比赛中,走线选取的好坏同样显得很重要。针对不同类型的赛道甚至赛道组合,走线的选取,既要考虑到走线路程的长短,还要考虑到相应的速度限制,因此,如何走线是一个值得研究的问题。在各种走线规划的策略中,一种最朴素而且效果也较明显的想法就是“抄近道”。所谓抄近道就是在小车不冲出赛道的前提下,使小车在赛道上沿尽可能短的路线前进。最典型的两种抄近道的表现方式如图1所示,即蛇形道(a)和单向弯(b)上的抄近道。
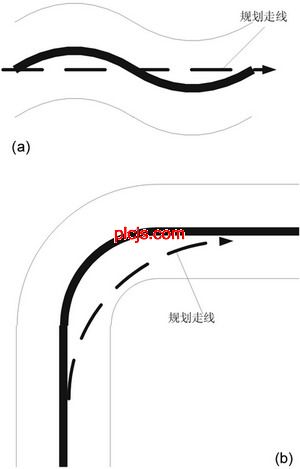
图1 智能车抄近道的两种方式
运动学模型和转向模型
运动学模型是描述智能小车位置、航向角、前轮转角之间动态变化关系的模型。转向模型是描述前轮转角自身变化时的动态关系的模型。
最优转角控制量求解
为描述方便,假设当前控制周期为kT周期,并假设kT、(k+1)T、……、(k+m)T周期的转角控制控制量依次为u(k)、u(k+ 1)、……、u(k+m),并假设(k+m)T周期以后的转角控制量为零(即车前轮正对着前方)。根据运动学模型和转向模型,可以推得智能小车在任一时刻的位置。设推算出的kT、(k+1)T、……、(k+P)T周期(通常取P>m)(即在未来(P+1)周期内)的智能小车的位置,依次为(x (k),y(k))、(x(k+1),y(k+1))、……、(x(k+P),y(k+P))。前面在走线规划时已经确定出了期望线路的位置,这样就可以求出未来(P+1)周期内每一周期智能小车与期望线路的位置偏差,记为d(k)、d(k+1)、……、d(k+P)。取一个正定的性能指标:
L
C
技
术
网
|
可
编
程
控
制
器
技
术
门
户
|
十
万
P
L
C
工
程
师
的
共
同
选
择
!